SESSION 9 | Introduction to Tree, Binary Tree and Expression Tree

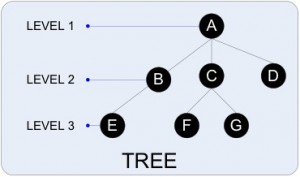
Tree

sebuah koleksi dari 1/banyak node.

Degree of tree : 3

Degree of C : 2

Height : 3

Parent of C : A

Children of A : B, C, D

Sibling of F : G

Ancestor of A : A, C

Descendant of C : F, G

Root : node paling atas

Edge : garis yang menghubungi parent dan child

Leaf : node yang tidak mempunyai anak

Sibling : node yang memiliki orang tua yang sama

Degree dari sebuah node : total dari sub tree sebuah node

Height/Depth : max degree dari node dalam tree

Jika ada garis yang menghubungkan p ke q, maka p adalah ancestor dari q dan q  adalah descendant dari p.

Binary Tree

tree yang akarnya harus memiliki minimal 2 anak.

Anak sebelah kiri disebut left child dan yang sebelah kanan disebut right child

Node yang tidak memiliki child disebut leaf.

Perfect binary tree : binary tree yang setiap levelnya memiliki depth yang sama

Complete binary tree : binary tree yang setiap levelnya, kecuali kemungkinan yang terakhir, terpenuhi, dan semua node berada di sebelah kiri. Perfect binary tree adalah sebuah complete binary tree.

Skewed binary tree : binary tree yang masing-masing nodenya memiliki hanya 1 anak.

Balanced binary tree : binary tree yang jarak root ke leaf sama dengan jarak antara anak kanan dan kiri.

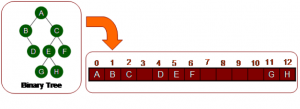
Representation of binary tree

Index dalam array menunjukan nomor node.

Index 0 adalah root node.

Index left child adalah 2p+1, dimana p adalah parent index.

Index right child adalah 2p+2.

Index parent adalah (p-1)/2.

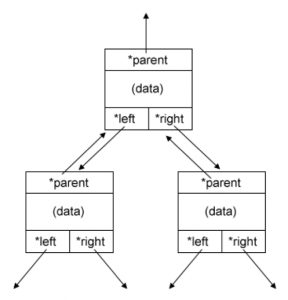
Contoh pake linked list :

struct node {

int data ;

struct node *left;

struct node *right;

struct node *parent;

}; struct node *root = NULL;

Expression tree concept 

prefix : *+ab/-cde

postfix : ab+cd-e/*

infix : (a+b)*((c-d)/e)

Kita dapat membuat expression tree dari prefix/postfix by recursive

Di prefix, harus print/process sebelum anak di proses.

Di postfix, harus print/process setelah anak di proses.